It is well documented that post hoc power calculations are not useful (Althouse, 2020; Goodman & Berlin, 1994; Hoenig & Heisey, 2001). Also known as observed power or retrospective power, post hoc power purports to estimate the power of a test given an observed effect size. The idea is to show that a “non-significant” hypothesis test failed to achieve significance because it wasn’t powerful enough. This allows researchers to entertain the notion that their hypothesized effect may actually exist; they just needed to use a bigger sample size. The problem with this idea is that post hoc power calculations are completely determined by the p-value. High p-values (i.e., non-significance) will always have low power. Low p-values will always have high power. Nothing is learned from post hoc power calculations.
In this article, we demonstrate this idea using simulations in R. To begin, let’s simulate some data and perform a t-test. We first draw 10 samples from two normal distributions. One has a mean of 10, and the other has a mean of 10.1. Therefore the “true” effect size is 0.1 (i.e., 10.1 - 10 = 0.1). Notice both also have the same variance. The set.seed(11) function allows us to always generate the same “random” data for this example. This allows you to follow along in case you want to replicate the result. It may help to pretend that we ran an experiment and that the x1 group is the control and the x2 group received some sort of treatment.
set.seed(11)
x1 <- rnorm(10, mean = 10, sd = 1)
x2 <- rnorm(10, mean = 10.1, sd = 1)
Next we run a t-test using the t.test() function. The t-test for these data returns a very high p-value of 0.72. If this were a real analysis, we would conclude that we’re unable to determine what effect, if any, exists. The 95% confidence interval on the difference in means ranges from -0.67 to 0.95. Every value in that range, including 0, is compatible with the data. The effect is almost certainly not exactly 0, but we can’t tell if the effect is positive or negative.
ttest <- t.test(x1, x2, var.equal = TRUE)
ttest
Two Sample t-test
data: x1 and x2
t = 0.3608, df = 18, p-value = 0.7224
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.6707225 0.9488640
sample estimates:
mean of x mean of y
9.769937 9.630867
Now let’s do a so-called post hoc power calculation using the observed effect. This is the observed difference in means. We can calculate power with the power.t.test() function. We need to give it delta (the effect, or difference in means), sd (the pooled standard deviation), n (sample size), and sig.level (the significance level or Type I error tolerance). We get the difference in means by calling the diff() function on the estimate element of the ttest object.
power.t.test(delta = diff(ttest$estimate),
sd = sqrt((var(x1) + var(x2))/2),
n = 10,
sig.level = 0.05,
type = "two.sample",
alternative = "two.sided")
Two-sample t test power calculation
n = 10
delta = 0.1390708
sd = 0.8618848
sig.level = 0.05
power = 0.05283998
alternative = two.sided
NOTE: n is number in *each* group
The post hoc power is calculated to be about 0.053, which is very low. Proponents of post hoc power might conclude that the experiment was under-powered, but as we stated in the opening, post hoc power is completely determined by the p-value. The experiment may very well be under-powered, but a post hoc power calculation doesn’t prove that. You will always get low post hoc power on a hypothesis test with a large p-value. The exercise is useless. Hoenig and Heisey (2001) demonstrate this mathematically. We’ll demonstrate it via simulation.
The replicate() function makes quick work of this. Simply pass our previous code (minus the set.seed() function) to replicate() as an expression surrounded by curly braces, and specify the number of times to replicate the code. Below we “replicate” the code 2000 times. The p-value of the test and post hoc power (or “observed power”) are returned in a vector. The results are stored in an object called sim_out.
sim_out <- replicate(n = 2000, expr = {
x1 <- rnorm(10, mean = 10, sd = 1)
x2 <- rnorm(10, mean = 10.1, sd = 1)
ttest <- t.test(x1, x2, var.equal = TRUE)
pwr <- power.t.test(delta = diff(ttest$estimate),
sd = sqrt((var(x1) + var(x2))/2),
sig.level = 0.05,
n = 10)
c(pvalue = ttest$p.value, obs_power = pwr$power)
})
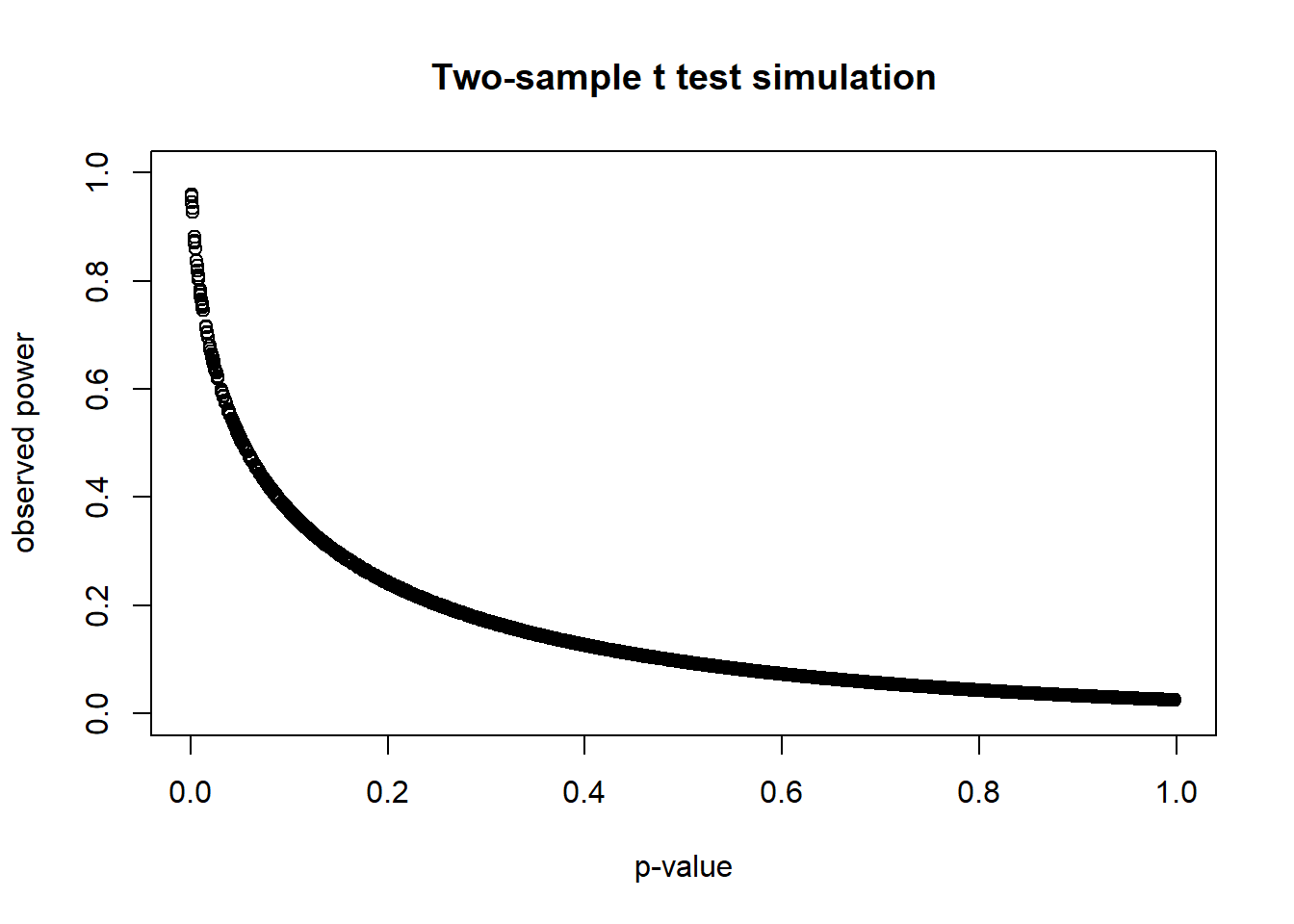
Next we create a scatterplot. Since the sim_out object has a dimension of 2 x 2000, we need to transpose it for easier plotting. We can do that with the t() function.
plot(t(sim_out),
xlim = c(0,1), ylim = c(0,1),
xlab = "p-value", ylab = "observed power",
main = "Two-sample t test simulation")
The resulting scatterplot reveals that high p-values always have low power and vice versa. The only time you’ll see high post hoc power is with a very small p-value. The point is you learn nothing new by calculating post hoc power.
We can demonstrate this with a chi-square test as well. Below we generate two groups labeled “A” and “B”, each with 40 members. Then we assign them probabilities of “success” of 0.5 and 0.7, respectively.
grp <- rep(c("A", "B"), each = 40)
p <- rep(c(0.5, 0.7), each = 40)
Next we use the rbinom() function to randomly return a 0 or 1 depending on the probability we give it. A 1 corresponds to treatment response; a 0 indicates no response. According to how we generated probabilities, group B should have more subjects respond. However, that doesn’t guarantee a chi-square test will detect that association, as we see below.
set.seed(2)
resp <- rbinom(n = length(grp), size = 1, prob = p)
table(grp, resp)
resp
grp 0 1
A 21 19
B 15 25
chisq.test(table(grp, resp))
Pearson's Chi-squared test with Yates' continuity correction
data: table(grp, resp)
X-squared = 1.2626, df = 1, p-value = 0.2612
We got a p-value of about 0.26. What’s the post hoc power of this test? We can calculate this by saving the results of the chi-square test, extracting the proportions, and using the power.prop.test() function. Notice we use the base R pipe operator, |>, introduced in version 4.1, to pass the observed counts to the proportions() function.
cout <- chisq.test(table(grp, resp))
obs <- cout$observed |> proportions(margin = 1)
power.prop.test(n = length(grp)/2,
p1 = obs["A","1"],
p2 = obs["B","1"],
sig.level = 0.05)
Two-sample comparison of proportions power calculation
n = 40
p1 = 0.475
p2 = 0.625
sig.level = 0.05
power = 0.2680786
alternative = two.sided
NOTE: n is number in *each* group
It should come as no surprise that a p-value of 0.26 leads to a low “observed power,” in this case about 0.27.
As we did with the t-test, we can replicate this many times and plot the p-values and post hoc power calculations.
sim_out <- replicate(n = 2000, expr = {
resp <- rbinom(n = length(grp), size = 1, prob = p)
chisqtest <- chisq.test(table(grp, resp))
obs <- chisqtest$observed |> proportions(margin = 1)
pwr <- power.prop.test(n = length(grp)/2,
p1 = obs["A","1"],
p2 = obs["B","1"],
sig.level = 0.05)
c(pvalue = chisqtest$p.value, obs_power = pwr$power)
})
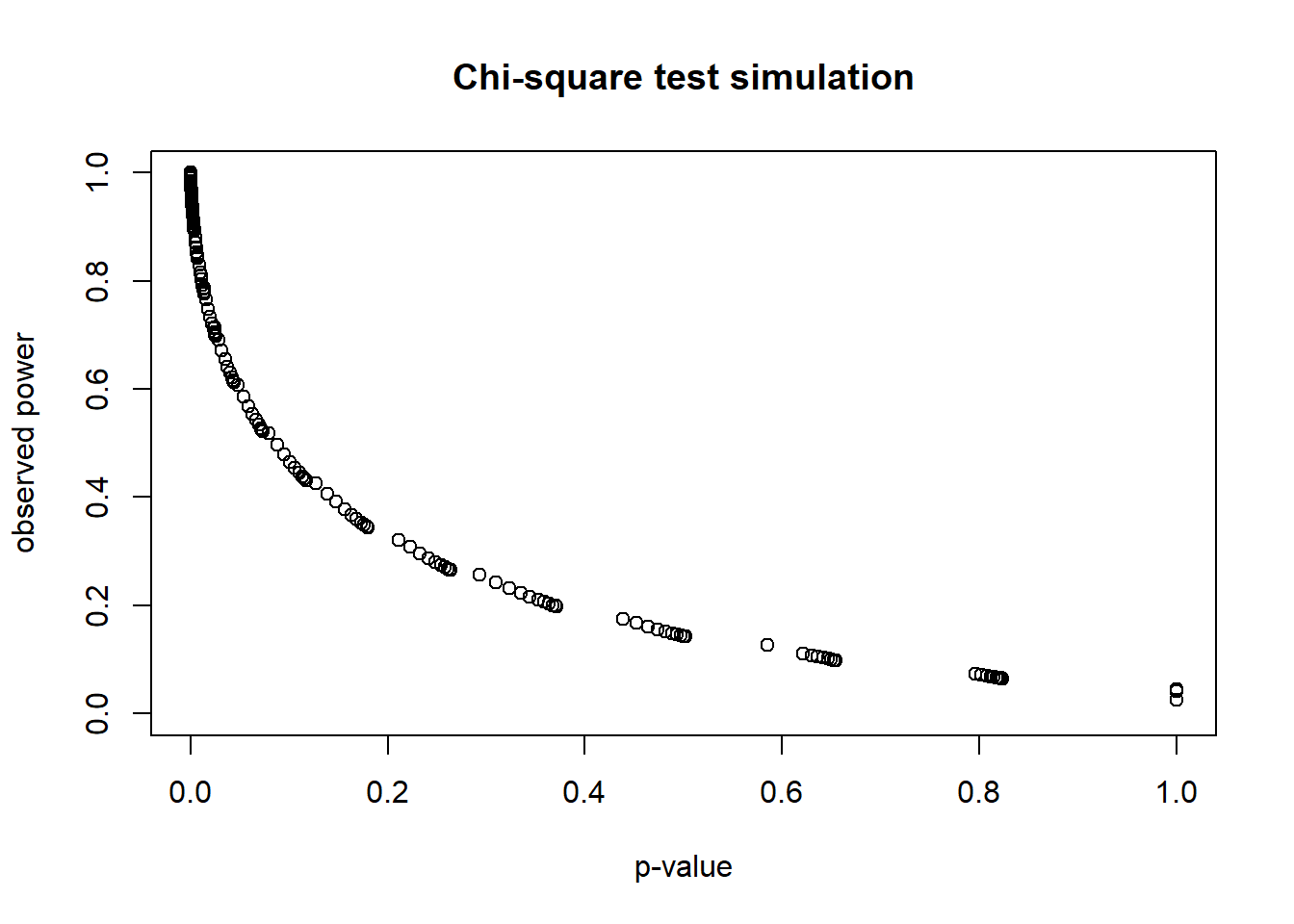
plot(t(sim_out),
xlim = c(0,1), ylim = c(0,1),
xlab = "p-value", ylab = "observed power",
main = "Chi-square test simulation")
Again, nothing is gained by performing post hoc power calculations. An insignificant result will always have low “power.” (The gaps in the scatterplot line are due to the discrete counts in the table.)
Power is something to think about before running an experiment, not after. Power is the probability of correctly rejecting a null hypothesis test when a hypothesized effect really exists. We pretend some meaningful effect is actually real and then determine the sample size we need to achieve a high level of power, such as 0.90.
In our first example, the real effect was 0.1 (with a standard deviation of 1). How large a sample size do we need to have a 90% chance of correctly rejecting the null hypothesis of no difference in the means at a significance level of 0.05? We can use the power.t.test() function to answer this.
power.t.test(delta = 0.1, sd = 1, sig.level = 0.05, power = 0.90)
Two-sample t test power calculation
n = 2102.445
delta = 0.1
sd = 1
sig.level = 0.05
power = 0.9
alternative = two.sided
NOTE: n is number in *each* group
It appears we need over 2100 subjects per group. Assuming our effect size estimates are realistic and meaningful, this provides us guidance on how many subjects we need to recruit. But it doesn’t guarantee a significant result. High power is a probability, not a certainty.
In addition to considering power before an experiment, we should focus less on p-values after the analysis and more on confidence intervals on the effect. There is a long tradition of making binary decisions of “some effect” or “no effect” based on a p-value falling below an arbitrary threshold. For example, get a p-value of 0.08 and declare there is “no effect” because the p-value is not less than 0.05. Or get a p-value of 0.000023 and declare a “highly significant effect” because the p-value is very small. In both cases, we’re making decisions about the effect without actually investigating the effect.
We previously ran a chi-square test on simulated data. Let’s do that again. Below we use set.seed(8) to allow you to replicate our result.
grp <- rep(c("A", "B"), each = 40)
p <- rep(c(0.5, 0.7), each = 40)
set.seed(8)
resp <- rbinom(n = length(grp), size = 1, prob = p)
chisq.test(table(grp, resp))
Pearson's Chi-squared test with Yates' continuity correction
data: table(grp, resp)
X-squared = 1.8569, df = 1, p-value = 0.173
The p-value of the chi-square test is 0.17. In a real analysis we might conclude “no effect,” since the p-value is greater than 0.05. But that decision doesn’t even consider the estimated effect. One way to estimate the effect is to calculate the difference in proportions between those who responded in group A and those who responded in group B, and then calculate a 95% confidence interval on the difference in proportions. This can be done with the prop.test() function. Before we do that, we use the table() and proportions() functions to determine that the observed effect is 0.675 - 0.500 = 0.175.
table(grp, resp) |> proportions(margin = 1)
resp
grp 0 1
A 0.500 0.500
B 0.325 0.675
To use the prop.test() function, the table needs to have “successes” in the first column and “failures” in the second column, so we swap the order of the columns. In addition, we swap the order of the rows so the estimated effect is B - A.
tab <- table(grp, resp)[c("B","A"),c("1","0")]
prop.test(x = tab)
2-sample test for equality of proportions with continuity correction
data: tab
X-squared = 1.8569, df = 1, p-value = 0.173
alternative hypothesis: two.sided
95 percent confidence interval:
-0.06231373 0.41231373
sample estimates:
prop 1 prop 2
0.675 0.500
Notice the p-value is exactly the sames as the chi-square test. (A chi-square test and a 2-sample proportion test are the same thing statistically speaking.) More importantly, notice the 95% confidence interval on the difference in proportions. Every proportion in that range is compatible with the data. Even though the p-value is “not significant,” plausible effects range from -0.06 to 0.4. To declare “no effect” is to decide that 0 is the most likely effect. But why is 0 more likely than 0.1 or 0.2? Instead of compressing this information into a single yes/no decision, we should report the confidence interval and let the reader see the range of plausible effect sizes.
R session details
Analyses were conducted using the R Statistical language (version 4.5.1; R Core Team, 2025) on Windows 11 x64 (build 26100)
References
- Althouse, A. (2021). Post Hoc Power: Not Empowering, Just Misleading. J Surg Res. Mar; 259:A3-A6.
- Goodman, SN, Berlin, JA. (1994). The use of predicted confidence intervals when planning experiments and the misuse of power when interpreting results. Ann Intern Med. 121:200-206.
- Hoenig, JM, Heisey, DM. (2001). The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat. 2001; 55:19-24.
- R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Clay Ford
Statistical Research Consultant
University of Virginia Library
August 4, 2021
For questions or clarifications regarding this article, contact statlab@virginia.edu.
View the entire collection of UVA Library StatLab articles, or learn how to cite.